CNN 参数更新
LeNet-51
结构
| Layer | Input Size | Kernel Size | padding | stride | Kernel Numbers | Output Size | Activation function |
|---|---|---|---|---|---|---|---|
| Conv1 | 32*32*1 | 5*5*1 | 0 | 1 | 6 | 28*28*6 | Sigmoid |
| Pool1 | 28*28*6 | 2*2 | 0 | 2 | 1 | 14*14*6 | Sigmoid |
| Conv12 | 14*14*6 | 5*5*? | 0 | 1 | 16 | 10*10*16 | Sigmoid |
| Pool2 | 10*10*16 | 2*2 | 0 | 2 | 1 | 5*5*16 | Sigmoid |
| Conv13 | 5*5*16 | 5*5*16 | 0 | 1 | 120 | 1*1*120 | Sigmoid |
| FC1 | 1*1*120 | 1*1*120 | - | - | 84 | 1*1*84 | - |
| FC2 | 1*1*84 | 1*1*84 | - | - | 10 | 1*1*10 | - |
Pool 层采用的是求和后乘以权值再加上偏置的方法,并不是常见的最大值池化
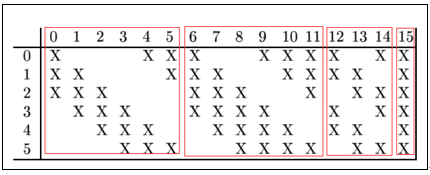
由于 Conv12 层的不同的卷积核所需要对应的通道数量不同,因此卷积核的尺寸并不固定
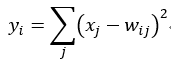
FC2 层是计算 FC2 层所有输出与特定权值之差的累计
可训练参数
Conv1 层的可训练参数为 (5 * 5 * 1 + 1) * 6 = 156,其中 5 * 5 是卷积核内的参数,1 是偏置系数
Pool1 层的可训练参数为 (1 + 1) * 6 = 12,其中的 1 + 1 分别是权值和系数
Conv2 层的可训练参数为 (5 * 5 * 3 + 1) * 6 + (5 * 5 * 4 + 1) * 6 + (5 * 5 * 4 + 1) * 3 + (5 * 5 * 6 + 1) * 1 = 1516
Pool2 层的可训练参数为 (1 + 1) * 16 = 32
Conv3 层的可训练参数为 (5 * 5 * 16 + 1) * 120 = 48120
FC1 层的可训练参数为 (120 + 1) * 84 = 10164
FC1 层的可训练参数为 84 * 10 = 840
总计需要训练 156 + 12 + 1516 + 32 + 48120 + 10164 + 840 = 60840 个参数
简化
| Layer | Input Size | Kernel Size | padding | stride | Output Size | Activation function | |
|---|---|---|---|---|---|---|---|
| Conv1 | 32*32*1 | 5*5*1 | 0 | 1 | 28*28*6 | ReLu | |
| Pool1 | 28*28*6 | 2*2*1 | 0 | 2 | 14*14*6 | ReLu | |
| Conv12 | 14*14*6 | 5*5*6 | 0 | 1 | 10*10*16 | ReLu | |
| Pool2 | 10*10*16 | 2*2*1 | 0 | 2 | 5*5*16 | ReLu | |
| Conv13 | 5*5*16 | 5*5*16 | 0 | 1 | 1*1*120 | ReLu | |
| Flatten | 1*1*120 | - | - | - | 120 | - | |
| FC1 | 120 | - | - | - | 84 | - | |
| FC2 | 4 | - | - | - | 10 | - |
- 卷积核其实是有深度的
- 输出的通道数就是卷积核的数量
- 同一个卷积核在不同深度的参数在很大程度上是不同的
- 同一个卷积核进行卷积时,卷积核的参数保持不变,这样每一处卷积的权重都是一致的,这就是 CNN 的权值共享,可以有效地减少参数量
参数更新与反向传播
CNN 的参数更新依赖梯度下降算法和反向传播算法
反向传播在这里主要是根据 Loss 反求偏导
$$\frac{\partial L}{\partial w} = \frac{\partial y}{\partial w} * \frac{\partial L}{\partial y}$$
梯度下降则是将参数减去学习率乘偏导
$$w' = w - rate * \frac{\partial L}{\partial w}$$
在最大池化层中,未被保留的部分偏导为 0
梯度消失
当卷积神经网络的层数很多时,反传上来的梯度/偏导的的值会变得很小,趋近于0
这将会严重影响 CNN 参数的更新,最终影响到网络的性能
为避免这种情况发生,何凯明提出了 ResNet2,在 CNN 中进行 shortcut ,提高偏导的绝对值,很好地解决了梯度消失的问题
Y. Lecun, L. Bottou, Y. Bengio, and P. Haffner. 1998. Gradient-based learning applied to document recognition. Proceedings of the IEEE 86, 11 (November 1998), 2278–2324. DOI:https://doi.org/10.1109/5.726791↩︎
Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2016. Deep Residual Learning for Image Recognition. 770–778. Retrieved March 27, 2023 from https://openaccess.thecvf.com/content_cvpr_2016/html/He_Deep_Residual_Learning_CVPR_2016_paper.html↩︎